
Figure 1: A Teeples cottage evening with stars of the northern sky on a blue background.
I have recently posted a series of notes about the efficiency of monochrome and colour cameras, considering how this varies with wavelength. I added some notes about the Sun’s emission and the absorption in our atmosphere, matters that also vary with wavelength.
I recently became aware that photographers of the lunar surface choose cameras and filters that block most of the visible light and pass the infra-red light. This choice of wavelength/colour struck me as very odd.
Why? Well, infra-red photons have longer wavelengths and lower energy. The aperture of the scope, measured in numbers of wavelengths is smaller, reducing resolution. If we are thinking of the telescope optics they should be doing the opposite.
The Dawes limit is an empirical measure of the resolving power of a telescope. Mr. Dawes arranged for people to view pairs of stars and had them identify the point where one star could not be distinguished from the other. It is strictly applicable only to a wavelength of 562 nm, which is in the middle of the visible spectrum.
The Rayleigh limit is very similar to the Dawes limit, and is based on more theoretical analysis. At the wavelength of 562 nanometers it is simply 22% greater than the Dawes limit.
“Rayleigh” is Mr. John William Strutt, 3rd Baron Rayleigh, a prolific English mathematician and scientist (1842-1919). His work in optics led to this theory of angular resolution, and he also did work on the scattering of light. He won the 1904 Nobel Prize in Physics for the discovery of Argon and for measuring the density of gasses.
The Rayleigh limit can be computed at different frequencies (unlike the Dawes limit).
Θ = 1.22 λ/D (in radians)
Where:
θ is the Rayleigh limit in radians
λis the wavelength of the incoming radiation/light
D is the aperture diameter.
1 radian = 206264.8 arcsec.
For D=11 inches (279.4mm), λ = 562 nm (0.000562mm), we get θ = 2.4575 *10^(-6) radians or 0.51 arcseconds. For λ =700 nm (0.0007 mm), we get θ = 3.0565 *10^(-6) radians or 0.63 arcsec.
A smaller value for the Rayleigh limit is better: We see finer structure in the object being viewed.
An example of this frequency dependence in action is through comparison of the Hubble Space Telescope with the James Webb Space Telescope. Their resolution in their main operating modes is limited by the optics (e.g. Rayleigh limit) and is roughly the same. The JWST has a much bigger aperture but the benefit (in terms of resolution) is lost because they are imaging using wavelengths of light in the infra-red.
To summarize, the resolution of a telescope (due to the optics) varies linearly with the wavelength. Small wavelengths (UV, for instance) give better resolution than longer ones (IR). Due to the optics, that is…
So why are the loony astrophotographers using IR wavelengths and filtering out most of the visible and UV light? You might as well ask why the sky is blue. It is a phenomenon that is yet another product of Rayleigh’s work… Rayleigh Scattering.
The sky is blue because the blue photons from the sun are scattered by particles in the atmosphere. The redder photons see much less scattering, and hence the sun appears yelllowish while the sky around it appears blue. This is Rayleigh Scattering. This atmospheric effect works against the blue and is less of a problem for the red.
The blue we see in the sky is a blend of the different wavelengths being scattered. Some green and red light is also scattered, but the overall colour is perceived as blue. If we were to take an elevator to an observation point above the Earth's atmosphere we would perceive our Sun as being white (more or less) and the sky as being black.
Starlight is affected in a similar way to the light from the Sun. Stars vary in their mass and frequency profiles of emission (e.g. the surface of red giant stars is cooler and therefore the emission is shifted to red wavelengths) but all are made more apparently "yellow" to Earthly observers by scattering. Stars are not bright enough for our eyes to detect this subtle colouration. Apparently in areas with little light pollution the sky around a bright moon will also appear blue, due to scattering of the moonlight, which is a reflection of the Sun's light.
There are different types of light scattering. Rayleigh scattering occurs when the size of particles in the atmosphere are much smaller (a factor of 10 or 15) than the wavelength of the light being scattered. The particles of interest are therefore not very big; 50nm across or smaller.
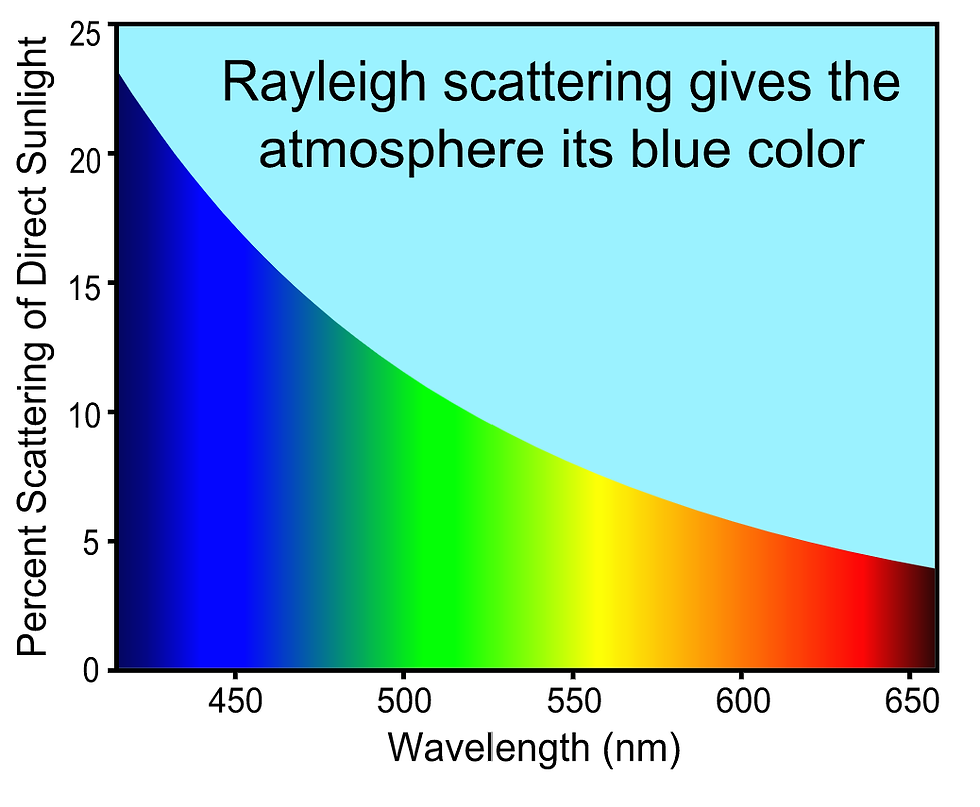
Figure 2: Rayleigh Scattering as a function of wavelength. Nearly 20% of Photons at 450nm wavelength are scattered, while less than 5% of those at 650nm suffer this fate. Image from Wikipedia.
There are specialized filters called "IR Pass" filters that block most visible light but allow the IR through. They have a passband from 650 (red) to 850nm (in the IR). The standard Astronomik "Deep Sky" red filter has a passband from around 600 to 700nm, stopping before the IR. This range of wavelengths seems to be where the curve flattens and little more is to be gained by going into the IR. The passband is smaller, so fewer photons will get through - this is something to assess when the time comes.
While researching this question I watched a YouTube video where a camera with high IR sensitivity was (1) operated with the IR Pass filter and (2) with no filter (allowing lots of IR, plus the visible light). The video presented images of the lunar surface side-by-side for comparison. I couldn't tell the difference!
Another question you may be asking is "who cares?", given that the atmospheric "seeing" is nearly always the limiting factor for resolution. The answer is that planetary and lunar imagers use a technique called "lucky imaging" that involves taking thousands of very rapid images, deleting 95% of these, and keeping the ones that were "lucky" enough to have not been corrupted by the atmosphere. In "lucky imaging" it is possible to reach the optical limits of the scope - if you're lucky. This works for very bright objects - our Moon and the planets.
I don't think it will matter very much what I do in terms of colour filters when imaging planets or the moon. My plan, once the skies clear, and once the moon rises to a location above the trees, and if the crick don't rise, is to use an Astronomik Red filter. I have a feeling that it will strike a good compromise between the optics and the Rayleigh scattering. Wish me luck!

Comentarios