(updated July 15, 2022 - L2 and pointing & more colourful information on frequencies)
If you’re like me, you get quite frustrated at the bad weather we experience here on the surface of this planet. All that moisture churning around above us, blocking the stars most of the time. Yuck.
I think it’s time to buy a space telescope. The latest model is one called the “James Webb Space Telescope” or JWST.
Yes, I know its very pricey. Let’s take a look anyway.

JWST, image courtesy of NASA
When we buy scopes for backyard Astro-photography we need to consider the desired field of view, we want to maximize the numbers of photons we collect from the desired targets, and we want to sample the image in the best way possible. I prefer to have systems that are “fast” – getting lots of photons into each pixel quickly.
We also need to buy mounts that accurately compensate for the Earth’s rotation - which is not needed if we get off this spinning planet.
Let’s look at the different considerations and compare the JWST to my existing RASA-11 scope.
Aperture:
My scope, the RASA-11, has an aperture (diameter) of 11” or 280mm. That scope is quite a beast to handle and I wouldn’t want to get one much bigger! When William Herschel built a giant 40 foot (focal length) telescope in the 1780s it was so difficult to handle that it was eventually abandoned. This pattern that has repeated over and over in history: It is only too common among amateurs!
The JWST aperture has a diameter of 6.5m or 6500mm. That’s 23 times bigger in diameter or 540 times bigger in area. Other things being equal (they are not) it would capture 540 times as many photons from the targets as my scope. It is quite a monster, but fortunately gravity is pretty much zero where it’s located.
Field of View:
This is quite interesting. My 11” RASA telescope (620mm focal length), coupled with the ZWO ASI 6200 camera, has a field of view of 3.3 degrees by 2.2 degrees. That’s quite large for a big scope. The JWST has a focal length of 131 meters. Yes, that’s correct, over 400 feet. William Herschel would die with envy. With the “Near Infrared Camera” in place (I believe this to be the main JWST camera) the field of view will be 130 arcseconds square, just over 2 minutes of arc on a side.
Here’s a comparison: the purple rectangle is the field of view of my RASA setup, and the tiny blue square is the JWST.

JWST Field of View compared to that of the RASA11/ASI6200 combination
The JWST is meant to look at very small objects, like far-away galaxies. The image below shows the JWST field of view with a small target, Jupiter. Looks great!

JWST Field of View shown with Jupiter
It will be quite limiting for other objects, that’s for sure. The next image shows how JWST would only see the core of Messier 51, the Whirlpool Galaxy.

JWST Field of View shown over M51, Whirlpool Galaxy
I was surprised at this tiny field of view because the Hubble Space Telescope has shown nice pictures of relatively large targets. The Hubble “Advanced Camera for Surveys”, wide-field mode, has a field of view of 202 arcseconds by 202 arcseconds. That’s not a wide-field to any amateur astronomer!
How does the Hubble team produce the larger images we see in the media? It seems that the trick is to take several pictures and merge them into a “mosaic” image. The image below is a Hubble image of just a small part of the Andromeda Galaxy. NASA says that this was the largest Hubble mosaic (as of 2015) and was “assembled together into a mosaic image using 7,398 exposures taken over 411 individual pointings”. Sounds like a lot of work. The next image shows what I’d expect with my RASA-11 (one “pointing”).

Hubble Andromeda Galaxy Mosaic of 411 images (Image courtesy of NASA)

RASA11 & ASI6200 Expected Field of View
Sampling:
For deep sky objects like galaxies and nebulae we want to sample all of the spatial structure of the target available to our view. Considering their stellar diameters and distance from us, (nearly all) stars should approximate perfectly sharp points of light (unresolved and unresolvable). Unfortunately, there are two main problems that reduce that sharpness.
First are limitations from the optics and the aperture. The Dawes limit is a measure of how spread out a star will be simply due to the optics. For an 8” diameter aperture telescope the Dawes limit (at visible light wavelengths) is 0.57 arcseconds. For a smaller scope with an aperture diameter of 60mm this limit becomes 1.93 arcseconds.
360 degrees make a full circle. Each degree has 60 arc-minutes and each arc-minute has 60 arcseconds. There are 3600 arcseconds in a degree. An arcsecond is quite a small angle.
The spread of a star is usually measured by something called the Full-Width Half Max or FWHM. A star will have a brightness profile something like a Gaussian: The FWHM is the (full) width of the star’s brightness profile (“Point Spread Function”) at a point half way to the top (half of the maximum).
For larger scopes planted on the Earth’s surface the primary concern is the atmospheric seeing – basically blurring of the targets due to atmospheric turbulence. Observatories on carefully chosen mountain tops can get this “seeing” to better than 1 arcsecond, but I doubt very much if it is ever below 2 or 3 arcseconds at Lac Teeples.
In the real world we also deal with imperfect focus, shaky equipment, various mount problems and blunders that I like to blame on others. I'm not sure but I suspect that terrestrial observers in the real world generally won’t get stars sharper than 3 arcseconds FWHM.
If that’s the limit of the spatial structure of your target then you will want to sample that at the famous Nyquist 2x rate (or thereabouts). So, for this 3 arcseconds FWHM example you want each (square) pixel of your camera to observe 1.5 arcseconds by 1.5 arcseconds of the sky. Astro-photographers have a rule of thumb that this “pixel scale” should be between 1 and 2 arcseconds per pixel.
I should note that for brighter objects like the moon and major planets this rule doesn’t apply.
Comparing Sampling:
My RASA scope with the ASI6200 camera has (by design) a pixel scale of 1.25 arcseconds per pixel. That is, each square camera pixel is seeing a piece of the sky that is 1.25 arcseconds by 1.25 arcseconds. This is right in line with the Astro-photographers rule of thumb for deep sky objects (galaxies & nebulae). If the seeing is very good and everything is working and in focus (!) I could pick up spatial features at the scale of around 2.5 arcseconds in the target objects. I'm likely over sampling most (if not all) of the time.
The JWST telescope designers didn’t have to worry about the atmosphere or the Earth's rotation. Hopefully they have a reliable method of focusing! That “rule of thumb” certainly does NOT apply to a space telescope.
The designers simply looked at the limits imposed by the optics and selected instruments to ensure that no spatial structure in their target was lost. The JWST team notes that the Full Width Half Max (FWHM) of the Point Spread Function (PSF) is 0.064 arcseconds @ 2μm and 0.13 arcseconds @ 4μm. They further note that the pixel scale for their camera/scope combination represents Nyquist sampling for these values.
The JWST will be able to pick up fantastic fine detail, limited by the optics only. They will see structure in distant objects at around a tenth of an arcsecond. That’s something that no Earth-bound telescope can do because of the “seeing”. I should note for completeness that there are systems that partially overcome these limitations, including adaptive optics and optical interferometers.
The tiny pixel scale is, of course, a reason why the JWST (or Hubble) field of view is so small. Even with a budget of a few billion dollars you can’t have everything. That camera is picking up the very fine details rather than a big field of view. Owners of long focal length telescopes (like the Schmidt-Cassegrain) will be familiar with this trade off.
How Fast is that thing?
Fast Optics are those that produce an image more quickly. This means that more of the target’s photons are hitting your camera’s pixels per unit of time than for slow optics. The measure of this is called the f-ratio. For my RASA-11 the f-ratio is an extraordinarily fast f/2.2. This is associated with the wide field of view and short focal length. In addition to the 11” aperture the camera (and each pixel of the sensor) sees a lot of the sky, and therefore images form quickly.
For comparison the 11” Schmidt Cassegrain telescope has a much longer focal length and a much smaller field of view. The aperture is the same as my RASA but it is only collecting photons from a very much smaller patch of the sky. It is a slow f/10.
What about the JWST? The f-ratio is simply the aperture over the focal length. The primary mirror aperture is 6.5m and the focal length is an amazing 131.4 meters, giving us a focal ratio of f/20, which is SLOW. For all that aperture, the extremely long focal length means that the telescope will be looking at such tiny parts of the sky that it will be slow to form images. The lack of a messy atmosphere may speed things up a bit though (no absorption or Rayleigh Scattering).
Frequencies:
Most astro-photographers have limited options when it comes to frequencies because they use cameras that are designed for visible light. The cameras may be sensitive to bands outside the visible (IR and UV), but this is fairly limited. Furthermore the telescopes themselves have limits: The RASA-11 specifications define a usable frequency range of 400nm to 700nm (visible light). I suspect this is because the RASA utilizes a lens which would act differently on different frequencies (mirrors don't have this problem).
We use filters within that frequency range to form RGB images, eliminate light pollution or pick up specific types of emission (a favourite is the Hydrogen-Alpha spectral line). Some lunar and planetary photographers eliminate all frequencies outside a band in the Red to IR. The Earth's atmosphere also reduces some frequencies of light reaching our cameras due to absorption (keeping us out of the UV, for example). Finally we have Rayleigh Scattering to contend with, causing us to lose a lot of the blue light (which scatters around the sky, making the sky blue).
The JWST is designed to work in the infra-red spectrum, NOT in the usual visible spectrum. A typical human eye will respond to wavelengths from about 380 to about 750nm (nanometers) while the JWST will be sensitive to 600nm through 28,500nm.
I wondered about the astronomer’s favourite, the Hydrogen-Alpha spectral line. H-alpha (Hα) is a specific deep-red visible spectral line with a wavelength of 656.28 nm. The JSWT is indeed sensitive to that line but no blue or purple colours will be seen.
By looking at entirely different frequencies JWST will be able to see different phenomena compared to instruments working in the visible spectrum. The IR is known to be useful to observe star-forming regions and we know that the most distant objects in the universe will be red-shifted in the direction of the JWST's sensitivity.
The data will be unique and it’s hard for me to say what will appear.
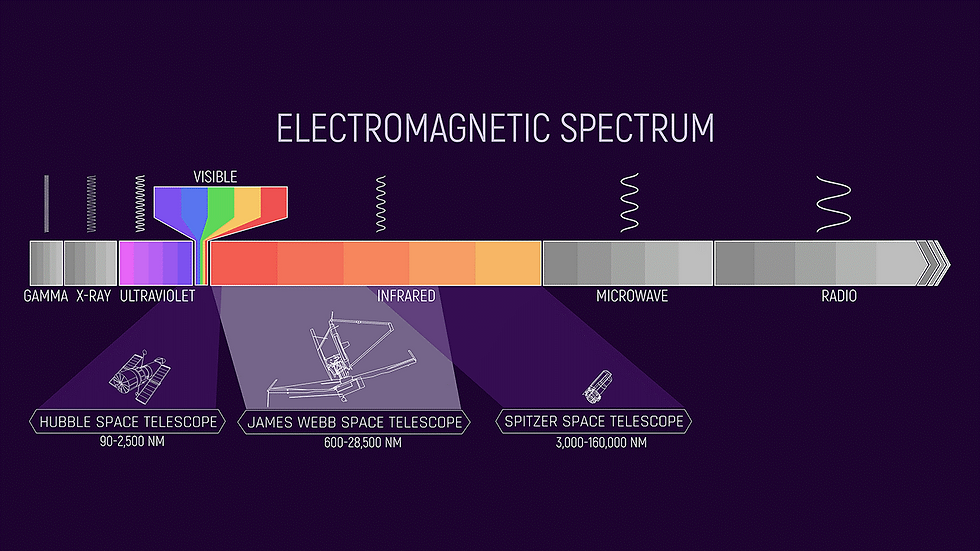
Spectrum covered by various Space Telescopes (courtesy of NASA)
Pointing:
We noted earlier that a telescope on the Earth's surface needs to compensate for the Earth's diurnal rotation, an activity called "tracking". For many astronomers the tracking performed by their telescope mount is inadequate and they have a separate control loop using a "guide scope" and guiding software.
The rotation rate we have to compensate for is roughly 361 degrees per 24 hours (relative to inertial space). This is roughly 15 degrees per hour or 900 arcseconds/minute. My photographs typically involve exposures (subframes) lasting one minute of time, and I want to maintain pointing at around 1 arcsecond during that one minute of time. Therefore I want the tracking to be accurate to one part in a thousand - 900 arcseconds in a minute, NOT 899 or 901!
The JWST telescope is not entirely free from tracking and associated corrections.
The satellite will be in the Lagrange point #2, basically in an orbit about the Sun/Earth combination. The L2 orbit is synchronized with the orbit of the Earth around the Sun, so it is always in line with the sun and planet. It has to be at a particular distance out and must have a particular speed to maintain this orbit - it is basically in free-fall towards the combined mass of the Sun and Earth, but is moving fast enough that the actual distance from the mass center doesn't change.

NASA image of the Lagrange 2 location and the JWST.
The JWST needs to be pointed precisely at a target, and then the telescope needs to keep pointing at that target. To do so it is necessary to deal with different torques on the body of the satellite that would cause it to point away from the chosen target. For the JWST it is mainly a result of solar radiation pressure pushing on one side more than another. This is dealt with using "reaction wheels" which accumulate momentum until they themselves must be cleared (using thrusters). Overall, though, the JWST has to do far less pointing compensation than is required by a telescope on the Earth's surface.
Other Operational Considerations:
At the beginning of this post I noted my displeasure with the bad weather here on Earth. At my cottage observatory our local star - the sun - is ruining the observations more than half the time. Of the nights, only a small fraction of these are clear enough to observe (perhaps 20%). Then we need to consider the Earth's Moon which ruins half the nights. There is also that vast number of artificial satellites that leave traces in images. It's surprising that any imaging gets done at all!
Although the JWST will be optically “slow”, at least it will not be shut down by the sun or moon’s presence in the sky, nor will it lose time due to cloud cover or satellites. Atmospheric absorption and Rayleigh Scattering don't exist. Space telescopes are definitely the way to go.
Final words:
The JWST is an interesting large-aperture, tiny field-of-view, weird-frequency scope. I would certainly buy one if I had the cash. Alas, I do not.
If you wish to donate a few hundred million dollars to a space telescope project, let me know! I’ve got some good design ideas already!
NOTE: the field of view calculations shown above were produced by the Astronomy Tools website: astronomy.tools.

Comentarios